-
-
[翻译]DeepSeekMath:推动开放语言模型中数学推理的极限
-
发表于: 2025-2-14 15:39 3791
-
数学推理对语言模型来说是一个重大挑战,因为它具有复杂且结构化的特性。在本论文中,我们介绍了 DeepSeekMath 7B,该模型是在 DeepSeek-Coder-Base-v1.5 7B 的基础上继续预训练的,使用了 1200 亿 由 Common Crawl 采集的数学相关标记(tokens),并结合了自然语言和代码数据。DeepSeekMath 7B 在 MATH 竞赛级基准测试上取得了 51.7% 的高分,且未依赖外部工具和投票技术,其表现接近 Gemini-Ultra 和 GPT-4。当使用 64 个样本的自洽性评估 时,DeepSeekMath 7B 在 MATH 上达到了 60.9%。
DeepSeekMath 出色的数学推理能力归功于两个关键因素:
充分挖掘了公共网络数据的潜力,通过精心设计的数据筛选流程,提取高质量的数学数据。
引入了 GRPO(Group Relative Policy Optimization),这是一种 PPO(Proximal Policy Optimization) 的变体,能在提升数学推理能力的同时优化 PPO 的内存使用。
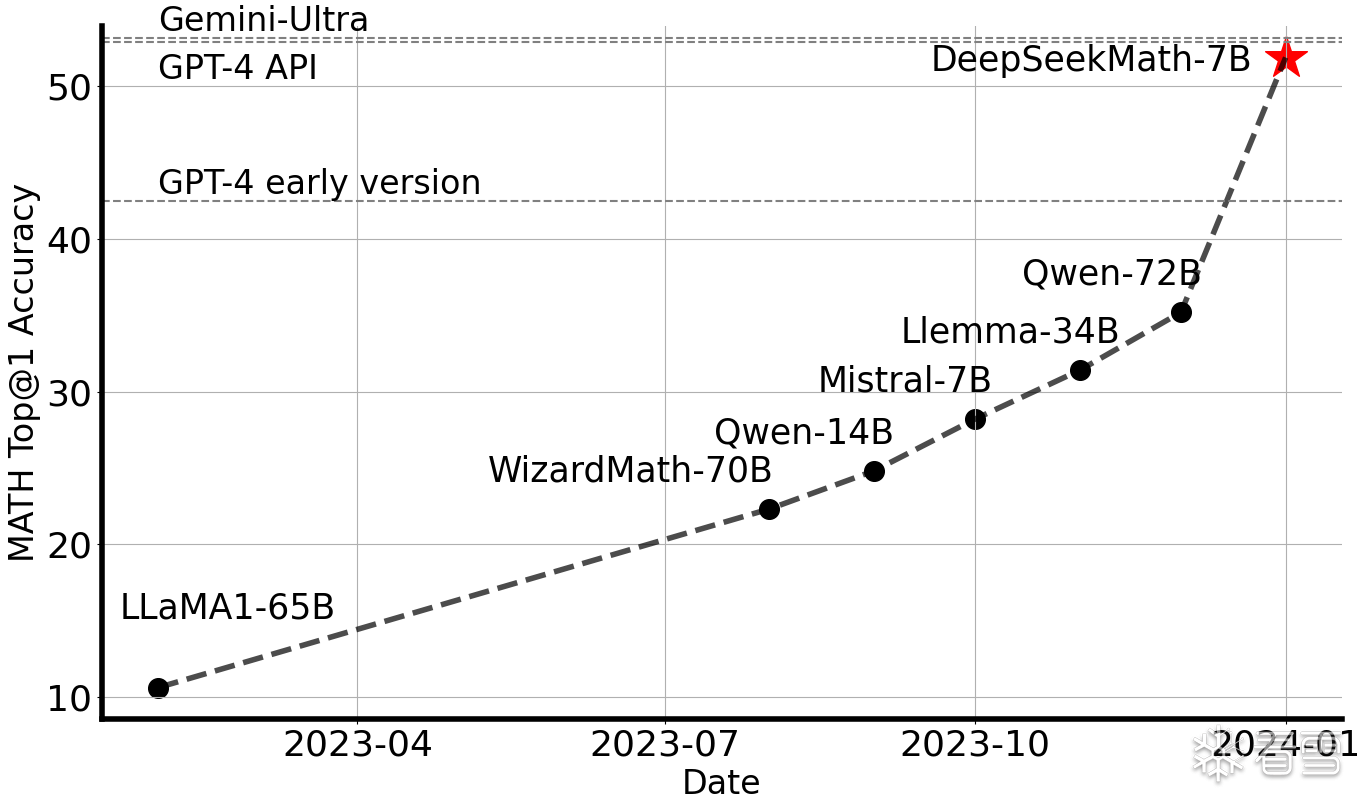
图1 开源模型在竞赛级MATH基准(Hendrycks等,2021)上的Top1准确率,未使用外部工具包和投票技术
引言
大语言模型(LLM)在人工智能数学推理方面带来了革命性的进展,推动了定量推理基准(Hendrycks 等,2021)和几何推理基准(Trinh 等,2024)的发展。此外,这些模型在帮助人类解决复杂数学问题(Tao,2023)方面也发挥了重要作用。然而,GPT-4(OpenAI,2023) 和 Gemini-Ultra(Anil 等,2023) 等最先进的模型尚未公开,而现有的开源模型在性能上仍远远落后。
本研究提出了 DeepSeekMath,一个领域特定(数学)的大语言模型,其数学能力远超现有开源模型,并接近 GPT-4 在学术基准上的表现。为实现这一目标,我们构建了 DeepSeekMath 语料库,一个大规模、高质量的数学预训练数据集,包含 1200 亿数学标记。该数据集通过 fastText 分类器(Joulin 等,2016)从 Common Crawl(CC) 中提取。分类器的训练过程如下:
- 初始版本的分类器以 OpenWebMath(Paster 等,2023) 的实例作为正样本,并从各种网页中选取负样本进行训练。
- 训练好的分类器用于挖掘 CC 中的更多正样本,这些样本随后经过人工标注进一步优化。
- 经过优化后的数据用于更新分类器,以进一步提升其筛选能力。
评估结果表明,该大规模语料库质量较高。例如,我们的基础模型 DeepSeekMath-Base 7B 在 GSM8K(Cobbe 等,2021)上达到了 64.2%,在 MATH 数据集(Hendrycks 等,2021)上达到了 36.2%,超越了 Minerva 540B(Lewkowycz 等,2022a)。此外,DeepSeekMath 语料库是多语言的,我们在中文数学基准(Wei 等,2023;Zhong 等,2023)上也观察到了性能提升。这表明,我们在数学数据处理方面的经验可为研究社区提供借鉴,并且未来仍有很大的改进空间。
DeepSeekMath-Base 以 DeepSeek-Coder-Base-v1.5 7B(Guo 等,2024) 作为初始模型,因为我们发现从代码训练模型出发比从通用 LLM 开始效果更好。此外,我们观察到数学训练不仅提升了模型在数学任务上的表现,还提高了其在 MMLU(Hendrycks 等,2020) 和 BBH(Suzgun 等,2022) 基准上的能力,表明数学训练不仅增强了数学能力,还提升了模型的通用推理能力。
在预训练完成后,我们对 DeepSeekMath-Base 进行数学指令微调(Instruction-Tuning),包括:
- 链式思维(Chain-of-Thought, CoT)(Wei 等,2022);
- 程序式思维(Program-of-Thought)(Chen 等,2022;Gao 等,2023);
- 工具整合推理(Tool-Integrated Reasoning)(Gou 等,2023)。
最终的 DeepSeekMath-Instruct 7B 超越了所有 7B 级别的开源模型,并可与 70B 级别的开源指令微调模型媲美。
此外,我们提出了 Group Relative Policy Optimization(GRPO),这是一种 PPO(Schulman 等,2017) 的变体强化学习(RL)算法。GRPO 不使用 critic 模型,而是基于组得分(group scores)估算基准值,从而显著降低训练资源消耗。仅使用部分英文指令微调数据,GRPO 就能显著提升 DeepSeekMath-Instruct 的性能,包括:
- GSM8K:82.9% → 88.2%
- MATH:46.8% → 51.7%
- CMATH(中文数学基准):84.6% → 88.8%
此外,我们提供了一个统一范式来理解 RFT(Rejection Sampling Fine-Tuning)(Yuan 等,2023a)、DPO(Direct Preference Optimization)(Rafailov 等,2023)、PPO 和 GRPO 等方法。基于此,我们发现所有这些方法都可以被归类为直接或简化的强化学习技术。
我们还进行了广泛的实验,例如:
- 在线 vs. 离线训练
- 结果监督 vs. 过程监督
- 单轮 RL vs. 迭代式 RL
以深入探讨该范式的核心要素。最后,我们分析了为什么强化学习能提升指令微调模型的表现,并总结了未来可能的优化方向,以实现更高效的 LLM 强化学习。
贡献
大规模数学预训练
- 证明了 Common Crawl 数据对数学任务的价值,通过精心设计的数据筛选流程,我们构建了 DeepSeekMath 语料库,包含 1200 亿数学标记,其规模是 Minerva 数学网页数据的 7 倍,是 OpenWebMath 的 9 倍。
- DeepSeekMath-Base 7B 在数学任务上表现可比 Minerva 540B,表明参数数量并非数学推理能力的唯一关键因素,小模型也能通过高质量数据取得强大性能。
- 代码训练有助于数学推理,我们发现先进行代码训练,再进行数学训练可提升模型的数学解题能力,无论是否使用工具。
- 单独训练 arXiv 论文对数学基准无显著提升,尽管许多数学相关研究都使用 arXiv 论文作为训练数据,我们的实验表明其增益有限。
强化学习的探索与分析
- 提出 GRPO,一种高效的 RL 方法,无需 critic 模型,基于组得分估算基准值,大幅减少训练资源消耗。
- GRPO 显著增强了数学指令微调模型的表现,仅使用指令微调数据即可提升**数学任务和跨领域任务(如 CMATH)**的性能。
- 提出一个统一范式来理解 RFT、DPO、PPO 和 GRPO,并通过大量实验分析 RL 的核心要素。
- 总结了 RL 提升 LLM 性能的关键因素,并提出了优化方向,为未来强化学习的研究提供新思路。
评估与度量摘要
英语与中文数学推理:
我们对模型在英语和中文基准测试上的表现进行了全面评估,涵盖从小学到大学水平的数学问题。
英语基准测试包括 GSM8K (Cobbe et al., 2021)、MATH (Hendrycks et al., 2021)、SAT (Azerbayev et al., 2023)、OCW Courses (Lewkowycz et al., 2022a) 和 MMLU-STEM (Hendrycks et al., 2020)。
中文基准测试包括 MGSM-zh (Shi et al., 2023)、CMATH (Wei et al., 2023)、Gaokao-MathCloze (Zhong et al., 2023) 和 Gaokao-MathQA (Zhong et al., 2023)。
我们评估了模型在不使用工具的情况下生成完整文本解答的能力,同时也评估了其使用 Python 解决问题的能力。
在英语基准测试上,DeepSeekMath-Base 在性能上可与闭源模型 Minerva 540B (Lewkowycz et al., 2022a) 相媲美,并超越所有开源的基础模型(如 Mistral 7B (Jiang et al., 2023) 和 Llemma-34B (Azerbayev et al., 2023)),无论这些模型是否经过数学预训练,DeepSeekMath-Base 的表现均明显领先。
尤其在中文基准测试上,DeepSeekMath-Base 具有更强的能力,这可能是因为我们没有像以往的研究 (Azerbayev et al., 2023; Lewkowycz et al., 2022a) 那样仅收集英语数学预训练数据,而是纳入了高质量的非英语数据。
通过数学指令微调和强化学习,最终得到的 DeepSeekMath-Instruct 和 DeepSeekMath-RL 展现出卓越的性能,在 MATH 数据集(竞赛级别)上首次在开源社区内取得了超过 50% 的准确率。
形式化数学:
我们在 miniF2F (Zheng et al., 2021) 数据集上,使用 Isabelle (Wenzel et al., 2008) 作为证明助手,评估 DeepSeekMath-Base 在非正式到正式的定理证明任务(Jiang et al., 2022)上的表现。
DeepSeekMath-Base 在少样本自动形式化任务上表现优异。
自然语言理解、推理与代码能力:
为了全面评估模型的语言理解、推理和编程能力,我们在以下基准测试上评估了 DeepSeekMath-Base:
- MMLU (Hendrycks et al., 2020):包含 57 个不同学科的多项选择任务;
- BIG-Bench Hard (BBH) (Suzgun et al., 2022):由 23 个需要多步推理的高难度任务组成;
- HumanEval (Chen et al., 2021) 和 MBPP (Austin et al., 2021):广泛用于评估代码生成能力的基准测试。
数学预训练
数据收集与去污染
本节介绍如何从 Common Crawl 构建 DeepSeekMath 语料库的过程。
如图 2 所示,我们设计了一个迭代管道,系统化地从 Common Crawl 中大规模收集数学语料数据,起始阶段使用的是种子语料库(即一小部分高质量的数学相关数据集)。
值得注意的是,这种方法同样适用于其他领域,如代码数据收集。
首先,我们选择 OpenWebMath (Paster et al., 2023) 作为初始种子语料库。
然后,我们使用该语料库训练fastText 模型 (Joulin et al., 2016),以检索更多类似 OpenWebMath 的数学网页。具体方法如下:
- 从种子语料库中随机选取 50 万条数据作为正样本;
- 从 Common Crawl 中随机选取 50 万个网页作为负样本;
- 使用 fastText 进行训练,参数配置如下:
- 向量维度:256
- 学习率:0.1
- 词 n-gram 最大长度:3
- 词最少出现次数:3
- 训练轮数:3
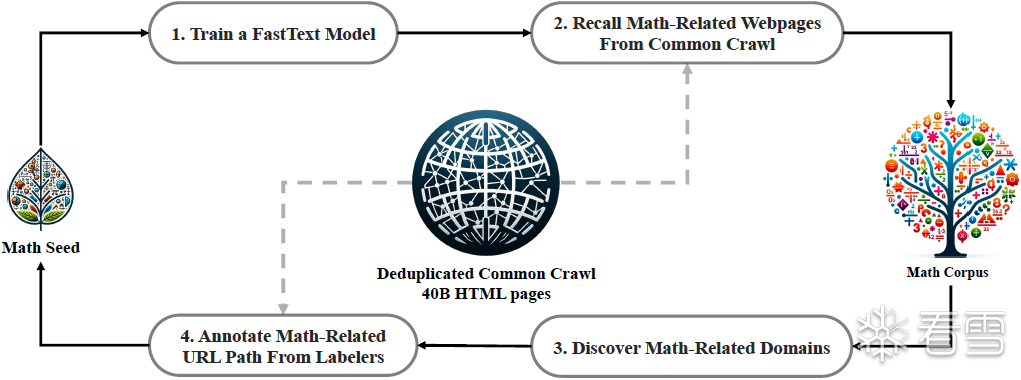
图2 一个从Common Crawl中收集数学网页的迭代流程
为了减少 Common Crawl 的数据规模,我们首先进行 URL 去重和近似去重,将网页数量减少到 400 亿。然后,我们使用fastText 模型从去重后的 Common Crawl 中召回数学网页。
为了过滤低质量的数学内容,我们按照 fastText 预测的分数对网页排名,仅保留排名靠前的数据。
我们在不同数据量(400 亿、800 亿、1200 亿和 1600 亿 tokens)上进行预训练实验,首轮选择保留 400 亿 tokens。
在第一轮数据收集后,仍有大量数学网页未被召回,主要原因是 fastText 模型的正样本多样性不足。因此,我们进一步扩充种子语料库:
- 将 Common Crawl 按域名划分(即相同基础 URL 的网页归为一类)。
- 计算每个域名中被召回的网页比例,如果某个域名超过 10% 的网页被召回,则将其归类为数学相关(如 mathoverflow.net)。
- 我们手动标注这些域名下的数学相关 URL(如 mathoverflow.net/questions)。
- 通过这些 URL 关联的未被召回的网页,将其加入种子语料库,优化 fastText 模型。
经过 四轮迭代,我们最终收集到 3550 万个数学网页,总计 1200 亿 tokens。
在第四轮时,我们发现98% 的数据已经在第三轮收集完成,因此决定停止数据采集。
为避免基准测试污染,我们遵循 Guo et al. (2024) 提出的方法,过滤掉包含英语与中文数学基准测试(如 GSM8K、MATH、CMATH、AGIEval)中题目或答案的网页:
- 如果某个文本段包含完整匹配的 10-gram 短语,该网页将被移除。
- 如果文本段长度小于 10-gram 但至少包含 3-gram,则采用精确匹配进行过滤。
验证 DeepSeekMath 语料库的质量
我们进行预训练实验,比较 DeepSeekMath 语料库 与其他数学预训练数据集:
- MathPile (Wang et al., 2023c):包含 89 亿 tokens,来源包括教科书、Wikipedia、ProofWiki、CommonCrawl、StackExchange 和 arXiv,其中 85% 以上来自 arXiv。
- OpenWebMath (Paster et al., 2023):从 CommonCrawl 过滤出的数学数据,共 136 亿 tokens。
- Proof-Pile-2 (Azerbayev et al., 2023):包含 OpenWebMath、AlgebraicStack(103 亿 tokens 数学代码)和 arXiv 论文(280 亿 tokens)。
训练设置
- 采用 DeepSeekLLM 1.3B(与 DeepSeek LLMs 框架相同)进行数学训练,每个数据集训练 1500 亿 tokens。
- 训练框架:HAI-LLM (High-flyer, 2023)。
- 优化器:AdamW (Loshchilov & Hutter, 2017),参数:
- β1=0.9, β2=0.95, weight_decay=0.1
- 学习率:最高 5.3e-4
- 批量大小:400 万 tokens,最大上下文长度:4K。
最终,DeepSeekMath 语料库在数学任务上展现出卓越的性能。
| 数学语料库 | 大小 | 英语测评 | 中文测试 | ||||||
| GSM8K | MATH | OCW | SAT | MMLUSTEM | CMATH | GaokaoMathCloze | GaokaoMathQA | ||
| No Math Training | N/A | 2.9% | 3.0% | 2.9% | 15.6% | 19.5% | 12.3% | 0.8% | 17.9% |
| MathPile | 8.9B | 2.7% | 3.3% | 2.2% | 12.5% | 15.7% | 1.2% | 0.0% | 2.8% |
| OpenWebMath | 13.6B | 11.5% | 8.9% | 3.7% | 31.3% | 29.6% | 16.8% | 0.0% | 14.2% |
| Proof-Pile-2 | 51.9B | 14.3% | 11.2% | 3.7% | 43.8% | 29.2% | 19.9% | 5.1% | 11.7% |
| DeepSeekMath Corpus | 120.2B | 23.8% | 13.6% | 4.8% | 56.3% | 33.1% | 41.5% | 5.9% | 23.6% |
表 1 DeepSeek-LLM 1.3B 在不同数学语料库上训练的性能,使用少样本链式思维提示进行评估。语料库大小是使用词汇量为 100K 的分词器计算的。
评估结果
DeepSeekMath 语料库质量高、涵盖多语言数学内容,并且规模最大。
- 高质量:我们在 8 个数学基准上使用少样本链式思维(Chain-of-Thought, CoT)提示(Wei 等,2022)来评估下游性能。如表 1 所示,使用 DeepSeekMath 语料库训练的模型在性能上有明显优势。图 3 显示,使用 DeepSeekMath 语料库训练的模型在 50B 训练 token(相当于 Proof-Pile-2 的 1 个完整训练周期)时表现优于 Proof-Pile-2,这表明 DeepSeekMath 语料库的平均质量更高。
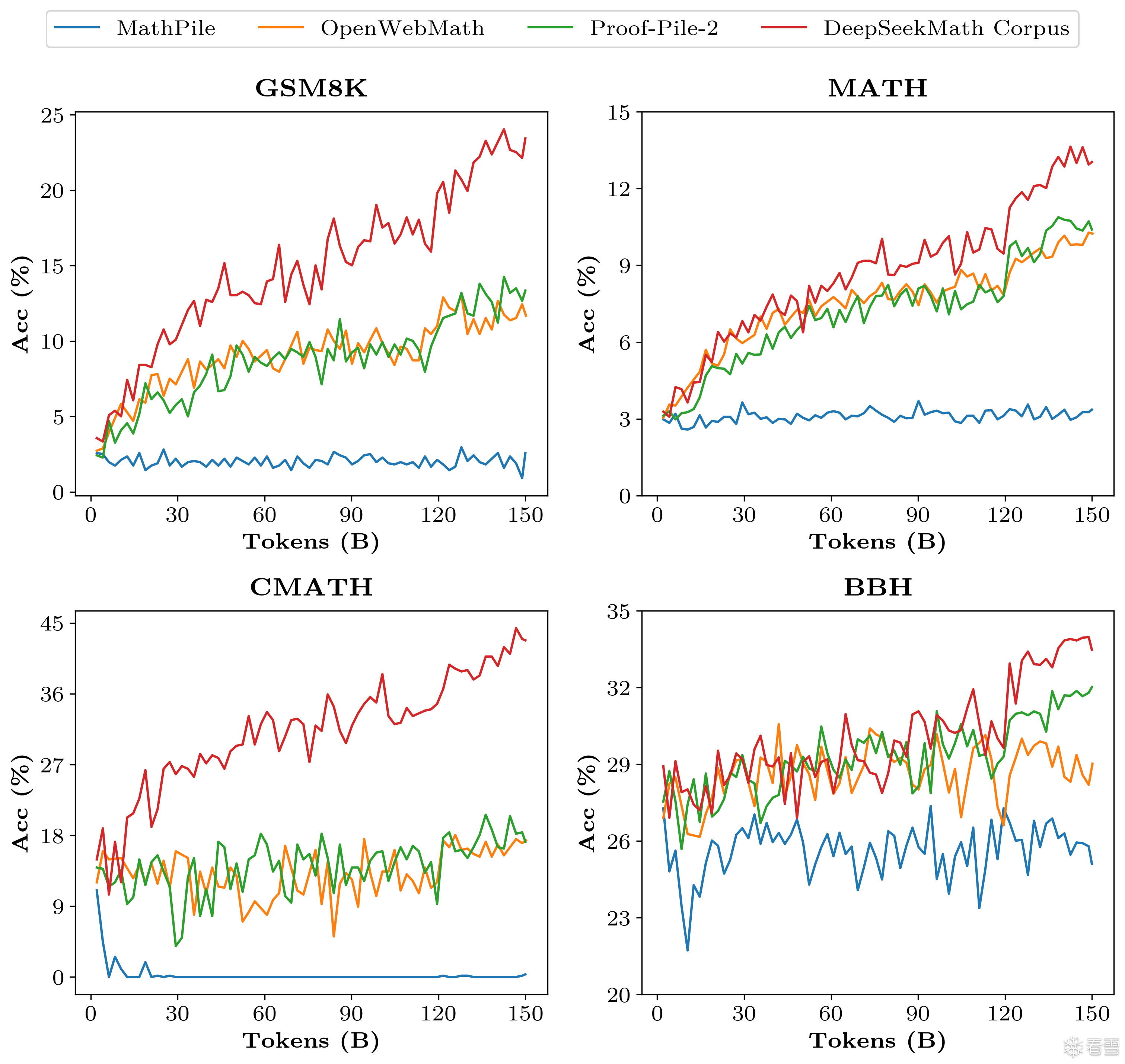
图3 在不同数学语料库上训练的DeepSeek-LLM 1.3B的基准曲线
- 多语言:DeepSeekMath 语料库包含多种语言的数据,主要以英语和中文为主。如表 1 所示,使用 DeepSeekMath 语料库训练的模型在英语和中文的数学推理能力上均有所提升。相比之下,现有的数学语料库主要以英语为主,不仅对中文数学推理能力提升有限,甚至可能导致性能下降。
- 大规模:DeepSeekMath 语料库的规模比现有的数学语料库大数倍。如图 3 所示,使用 DeepSeekMath 语料库训练的 DeepSeek-LLM 1.3B 具有更陡峭的学习曲线,并且改进更持久。相比之下,基线语料库规模较小,已经在训练过程中被重复多轮,使得模型性能很快达到瓶颈。
DeepSeekMath-Base 7B 的训练与评估
在本节中,我们介绍 DeepSeekMath-Base 7B,一个在数学推理方面表现卓越的基础模型。该模型以 DeepSeek-Coder-Base-v1.5 7B(Guo 等,2024)为初始化模型,并在 500B tokens 上进行训练。数据分布如下:
- 56% 来自 DeepSeekMath 语料库
- 4% 来自 AlgebraicStack
- 10% 来自 arXiv
- 20% 来自 Github 代码
- 10% 来自 Common Crawl 的英语和中文自然语言数据
我们主要采用 2.2.1 节 中的训练设置,但将学习率的最大值设为 4.2e-4,批量大小设为 10M tokens。
我们对 DeepSeekMath-Base 7B 进行了全面评估,重点考察其在以下方面的能力:
- 数学问题求解(不依赖外部工具)
- 使用工具进行数学问题求解
- 形式化定理证明
此外,我们还评估了模型在 自然语言理解、推理和编程 方面的性能。
数学问题求解与逐步推理
我们使用 少样本 CoT 提示 评估 DeepSeekMath-Base 7B 在 英语和中文数学基准 上的数学问题求解能力。测试基准包括:
- 数量推理(如 GSM8K (Cobbe 等, 2021)、MATH (Hendrycks 等, 2021) 和 CMATH (Wei 等, 2023))
- 多项选择题(如 MMLU-STEM (Hendrycks 等, 2020) 和 Gaokao-MathQA (Zhong 等, 2023))
这些基准涵盖了从 小学到大学水平 的数学问题。
如 表 2 所示,DeepSeekMath-Base 7B 在所有 8 个数学基准上均领先于其他开源基础模型(包括广泛使用的 Mistral 7B (Jiang 等, 2023) 和最近发布的 Llemma 34B (Azerbayev 等, 2023),后者在 Proof-Pile-2 语料库上进行了数学训练)。
值得注意的是,在 竞赛级数学基准 MATH 上,DeepSeekMath-Base 7B 比现有开源模型高出 10% 以上,甚至超越了 Minerva 540B (Lewkowycz 等, 2022a),后者是一个 封闭源模型,其规模比 DeepSeekMath-Base 7B 大 77 倍,基于 PaLM (Lewkowycz 等, 2022b) 并进一步在数学文本上训练。
| 模型 | 大小 | 英语测评 | 中文测评 | ||||||
| GSM8K | MATH | OCW | SAT | MMLUSTEM | CMATH | GaokaoMathCloze | GaokaoMathQA | ||
| 闭源模型 | |||||||||
| Minerva | 7B | 16.2% | 14.1% | 7.7% | - | 35.6% | - | - | - |
| Minerva | 62B | 52.4% | 27.6% | 12.0% | - | 53.9% | - | - | - |
| Minerva | 540B | 58.8% | 33.6% | 17.6% | - | 63.9% | - | - | - |
| 开源模型 | |||||||||
| Mistral | 7B | 40.3% | 14.3% | 9.2% | 71.9% | 51.1% | 44.9% | 5.1% | 23.4% |
| Llemma | 7B | 37.4% | 18.1% | 6.3% | 59.4% | 43.1% | 43.4% | 11.9% | 23.6% |
| Llemma | 34B | 54.0% | 25.3% | 10.3% | 71.9% | 52.9% | 56.1% | 11.9% | 26.2% |
| DeepSeekMath-Base | 7B | 64.2% | 36.2% | 15.4% | 84.4% | 56.5% | 71.7% | 20.3% | 35.3% |
表 2 DeepSeekMath-Base 7B 与强大的基础模型在英语和中文数学基准上的比较。模型使用链式思维提示进行评估。Minerva 的结果引用自 Lewkowycz 等人(2022a)
使用工具进行数学问题求解
我们在 GSM8K 和 MATH 上评估 程序辅助数学推理,并采用 少样本程序思维(program-of-thought)提示 (Chen 等, 2022; Gao 等, 2023)。
模型被提示通过编写 Python 程序 来解决数学问题,并可以使用 math 和 sympy 等库进行复杂计算。最终答案由程序的执行结果决定。
如 表 3 所示,DeepSeekMath-Base 7B 超越了先前的 SOTA 模型 Llemma 34B。
| 模型 | 大小 | 解决问题 w/Tools | 非正式到正式的证明 | ||
| GSM8K+Python | MATH+Python | miniF2F-valid | miniF2F-test | ||
| Mistral | 7B | 48.5% | 18.2% | 18.9% | 18.0% |
| CodeLlama | 7B | 27.1% | 17.2% | 16.3% | 17.6% |
| CodeLlama | 34B | 52.7% | 23.5% | 18.5% | 18.0% |
| Llemma | 7B | 41.0% | 18.6% | 20.6% | 22.1% |
| Llemma | 34B | 64.6% | 26.3% | 21.0% | 21.3% |
| DeepSeekMath-Base | 7B | 66.9% | 31.4% | 25.8% | 24.6% |
表3 基础模型在使用工具解决数学问题以及在Isabelle中进行非正式到正式定理证明的能力的少样本评估
形式化数学
自动化形式证明 有助于确保数学证明的准确性和可靠性,并提高效率,近年来受到越来越多的关注。
我们在 miniF2F (Zheng 等, 2021) 数据集上评估 DeepSeekMath-Base 7B 在 非正式数学证明自动形式化 任务上的表现。具体而言,模型需要根据 非正式陈述、正式陈述和非正式证明 生成一个 Isabelle 形式证明,并使用 少样本提示 进行推理。
按照 Jiang 等 (2022) 的方法,我们使用模型生成 证明草稿,然后调用自动证明工具 Sledgehammer (Paulson, 2010) 补全缺失的细节。
如 表 3 所示,DeepSeekMath-Base 7B 在 数学自动形式化 任务上表现出色。
| 模型 | 大小 | MMLU | BBH | HumanEval(Pass@1) | MBPP(Pass@1) |
| Mistral | 7B | 62.4% | 55.7% | 28.0% | 41.4% |
| DeepSeek-Coder-Base-v 1.5 | 7B | 42.9% | 42.9% | 40.2% | 52.6% |
| DeepSeek-Coder-Base-v 1.5 | 7B | 49.1% | 55.2% | 43.2% | 60.4% |
| DeepSeekMath-Base | 7B | 54.9% | 59.5% | 40.9% | 52.6% |
自然语言理解、推理与编程
我们在以下基准上评估 DeepSeekMath-Base 7B 的 自然语言理解、推理和编程能力:
- MMLU (Hendrycks 等, 2020) —— 评估 自然语言理解
- BBH (Suzgun 等, 2022) —— 评估 推理能力
- HumanEval (Chen 等, 2021) & MBPP (Austin 等, 2021) —— 评估 编程能力
如 表 4 所示,DeepSeekMath-Base 7B 在 MMLU 和 BBH 上相较于其前身 DeepSeek-Coder-Base-v1.5 (Guo 等, 2024) 有显著提升,表明数学训练对 语言理解和推理能力 具有积极影响。
此外,通过在训练中加入编程数据,DeepSeekMath-Base 7B 成功保持了 DeepSeek-Coder-Base-v1.5 在 HumanEval 和 MBPP 两个编程基准 上的性能。
总体而言,DeepSeekMath-Base 7B 在 推理和编程能力 上 显著超越了 Mistral 7B (Jiang 等, 2023)。
监督微调
SFT 数据策划
我们构建了一个数学指令微调数据集,涵盖了来自不同数学领域和不同复杂程度的英文和中文问题:这些问题与链式思维(CoT)(Wei et al., 2022)、程序思维(PoT)(Chen et al., 2022; Gao et al., 2023),以及工具集成推理格式(Gou et al., 2023)的解决方案配对。训练示例总数为 776K。
- 英文数学数据集:我们为 GSM8K 和 MATH 问题注释了工具集成解决方案,并采用了 MathInstruct(Yue et al., 2023)的一个子集以及 Lila-OOD(Mishra et al., 2022)的训练集,其中问题通过 CoT 或 PoT 解决。我们的英文集合涵盖了数学的多个领域,如代数、概率、数论、微积分和几何。
- 中文数学数据集:我们收集了涵盖 76 个子主题(如线性方程)的中文 K-12 数学问题,并以 CoT 和工具集成推理格式注释了解决方案。
深度搜索数学指令 7B 的训练和评估
在本节中,我们介绍了基于 DeepSeekMath-Base 进行数学指令微调的 DeepSeekMath-Instruct 7B。训练示例随机连接,直到达到最大上下文长度 4K 个标记。我们以批量大小 256 和恒定学习率 5e-5 训练模型 500 步。
我们在 4 个英文和中文的定量推理基准上评估模型的数学表现,无论是否使用工具。我们将我们的模型与当时的领先模型进行基准测试:
- 闭源模型包括:(1)GPT 系列,其中 GPT-4(OpenAI, 2023)和 GPT-4 代码解释器 2 是最强大的,(2)Gemini Ultra 和 Pro(Anil et al., 2023),(3)Inflection-2(Inflection AI, 2023),(4)Grok-1,以及最近由中国公司发布的模型,包括(5)Baichuan-3,(6)来自 GLM 系列的最新 GLM-4(Du et al., 2022)。这些模型用于一般用途,其中大多数经过了一系列的对齐程序。
- 开源模型包括:一般模型如(1)DeepSeek-LLM-Chat 67B(DeepSeekAI, 2024),(2)Qwen 72B(Bai et al., 2023),(3)SeaLLM-v2 7B(Nguyen et al., 2023),和(4)ChatGLM3 6B(ChatGLM3 Team, 2023),以及在数学上有所增强的模型,包括(5)InternLM2-Math 20B,它基于 InternLM2 进行数学训练后进行指令微调,(6)Math-Shepherd-Mistral 7B,它对 Mistral 7B 应用了 PPO 训练(Schulman et al., 2017)和过程监督的奖励模型,(7)WizardMath 系列(Luo et al., 2023),通过进化指令(即使用 AI 进化指令的指令微调版本)和 PPO 训练改进 Mistral 7B 和 Llama-2 70B 的数学推理,训练问题主要来自 GSM8K 和 MATH,(8)MetaMath 70B(Yu et al., 2023),它是 Llama-2 70B 在增强版 GSM8K 和 MATH 上进行微调的版本,(9)ToRA 34B Gou et al.(2023),它是 CodeLlama 34B 微调以进行工具集成的数学推理,(10)MAmmoTH 70B(Yue et al., 2023),它是 Llama-2 70B 在 MathInstruct 上进行指令微调的版本。
如表 5 所示,在禁止使用工具的评估设置下,DeepSeekMath-Instruct 7B 展现出强大的逐步推理能力。值得注意的是,在竞赛级别的 MATH 数据集上,我们的模型比所有开源模型和大多数专有模型(如 Inflection-2 和 Gemini Pro)至少高出 9% 的绝对值。即使对于那些规模更大(如 Qwen 72B)或通过以数学为中心的强化学习专门增强的模型(如 WizardMath-v1.1 7B),这一点也是如此。虽然 DeepSeekMath-Instruct 在 MATH 上可以与中国专有模型 GLM-4 和 Baichuan-3 相媲美,但仍不如 GPT-4 和 Gemini Ultra。
在允许模型集成自然语言推理和基于程序的工具使用来解决问题的评估设置下,DeepSeekMath-Instruct 7B 在 MATH 上的准确率接近 60%,超过了所有现有的开源模型。在其他基准上,我们的模型与 DeepSeek-LLM-Chat 67B 相竞争,这是之前的最先进模型,其规模是我们的 10 倍。
强化学习
群体相对策略优化
强化学习(RL)已被证明在监督微调(SFT)阶段之后进一步提高 LLM 的数学推理能力是有效的(Luo et al., 2023; Wang et al., 2023b)。在本节中,我们介绍我们高效且有效的 RL 算法,群体相对策略优化(GRPO)。
从 PPO 到 GRPO
近端策略优化(PPO)(Schulman et al., 2017)是一种广泛用于 LLM 的 RL 微调阶段的 actor-critic RL 算法。特别地,它通过最大化以下代理目标来优化 LLM:
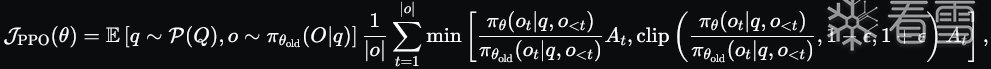
其中 πθ 和 πθold 是当前和旧的策略模型,q,o_q_,o 是从问题数据集和旧策略 πθold_πθ_old 中采样的问题和输出。 ϵ 是在 PPO 中引入的用于稳定训练的剪切相关超参数。 At 是优势,通过应用广义优势估计(GAE)(Schulman et al., 2015)计算,
| 模型 | 大小 | 英文测评 | 中文测评 | ||
| GSM8K | MATH | MGSM-zh | CMATH | ||
| 思维链推理 | |||||
| 闭源模型 | |||||
| Gemini Ultra | - | 94.4% | 53.2% | - | - |
| GPT-4 | - | 92.0% | 52.9% | - | 86.0% |
| Inflection-2 | - | 81.4% | 34.8% | - | - |
| GPT-3.5 | - | 80.8% | 34.1% | - | 73.8% |
| Gemini Pro | - | 86.5% | 32.6% | - | - |
| Grok-1 | - | 62.9% | 23.9% | - | - |
| Baichuan-3 | - | 88.2% | 49.2% | - | - |
| GLM-4 | - | 87.6% | 47.9% | - | - |
| 开源模型 | |||||
| InternLM2-Math | 20B | 82.6% | 37.7% | - | - |
| Qwen | 72B | 78.9% | 35.2% | - | - |
| Math-Shepherd-Mistral | 7B | 84.1% | 33.0% | - | - |
| WizardMath-v1.1 | 7B | 83.2% | 33.0% | - | - |
| DeepSeek-LLM-Chat | 67B | 84.1% | 32.6% | 74.0% | 80.3% |
| MetaMath | 70B | 82.3% | 26.6% | 66.4% | 70.9% |
| SeaLLM-v2 | 7B | 78.2% | 27.5% | 64.8% | - |
| ChatGLM3 | 6B | 72.3% | 25.7% | - | - |
| WizardMath-v1.0 | 70B | 81.6% | 22.7% | 64.8% | 65.4% |
| DeepSeekMath-Instruct | 7B | 82.9% | 46.8% | 73.2% | 84.6% |
| DeepSeekMath-RL | 7B | 88.2% | 51.7% | 79.6% | 88.8% |
| 工具综合推理 | |||||
| 闭源模型 | |||||
| GPT-4 Code Interpreter | - | 97.0% | 69.7% | - | - |
| 开源模型 | |||||
| InternLM2-Math | 20B | 80.7% | 54.3% | - | - |
| DeepSeek-LLM-Chat | 67B | 86.7% | 51.1% | 76.4% | 85.4% |
| ToRA | 34B | 80.7% | 50.8% | 41.2% | 53.4% |
| MAmmoTH | 70B | 76.9% | 41.8% | - | - |
| DeepSeekMath-Instruct | 7B | 83.7% | 57.4% | 72.0% | 84.3% |
| DeepSeekMath-RL | 7B | 86.7% | 58.8% | 78.4% | 87.6% |
表5 开源和闭源模型在英语和中文基准测试中使用链式思维和工具集成推理的表现。灰色分数表示32个候选者的多数票;其他为Top1分数。DeepSeekMath-RL 7B优于所有从7B到70B的开源模型,以及大多数闭源模型。尽管DeepSeekMath-RL 7B仅在GSM8K和MATH的链式思维格式指令微调数据上进行了进一步训练,但它在所有基准测试中都优于DeepSeekMath-Instruct 7B
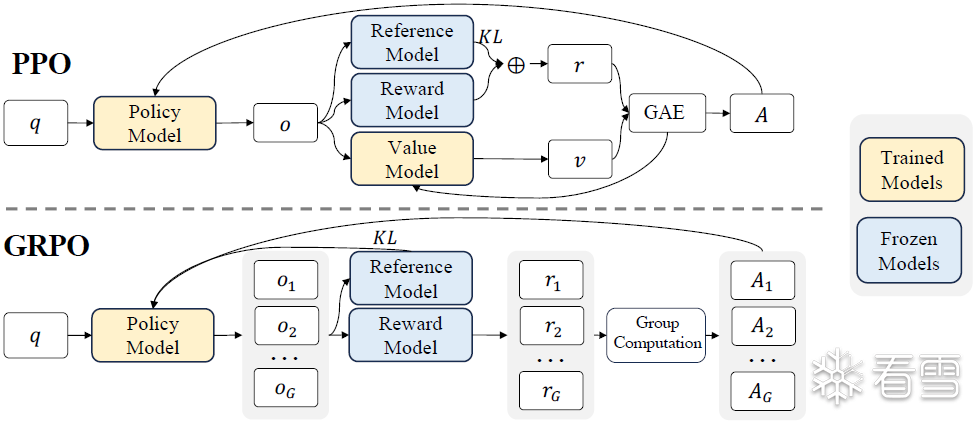
图4 PPO和我们的GRPO的演示。GRPO放弃了价值模型,而是通过组评分来估计基线,从而显著减少训练资源
基于奖励 {r≥t} 和学习的价值函数 Vψ。因此,在 PPO 中,需要一个与策略模型规模相当的价值函数进行训练,并且为了减轻奖励模型的过度优化,标准方法是在每个标记的奖励中添加来自参考模型的每个标记 KL 惩罚(Ouyang et al., 2022),即:

其中 rϕ 是奖励模型,πref 是参考模型,通常是初始 SFT 模型,β 是 KL 惩罚的系数。
由于 PPO 中使用的价值函数通常是与策略模型规模相当的另一个模型,这带来了巨大的内存和计算负担。此外,在 RL 训练期间,价值函数在计算优势时被视为基线以减少方差。而在 LLM 的情况下,通常只有最后一个标记由奖励模型分配奖励分数,这可能会使得训练一个在每个标记上都准确的价值函数变得复杂。为了解决这个问题,如图 4 所示,我们提出了群体相对策略优化(GRPO),它不需要像 PPO 那样额外的价值函数近似,而是使用对同一问题的多个采样输出的平均奖励作为基线。更具体地说,对于每个问题 q,GRPO 从旧策略 πθold 中采样一组输出 {o1,o2,⋯ ,oG},然后通过最大化以下目标优化策略模型:
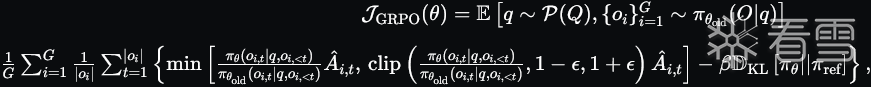
其中 ϵ 和 β 是超参数,A_^_i,_t_ 是仅基于每个组内输出的相对奖励计算的优势,这将在以下小节中详细介绍。GRPO 利用群体相对方式计算优势,与奖励模型的比较性质很好地对齐,因为奖励模型通常是在同一问题上输出之间的比较数据集上训练的。还需要注意的是,GRPO 通过直接将训练的策略和参考策略之间的 KL 散度添加到损失中进行正则化,而不是在奖励中添加 KL 惩罚,从而避免了复杂化 A_^_i,_t_ 的计算。
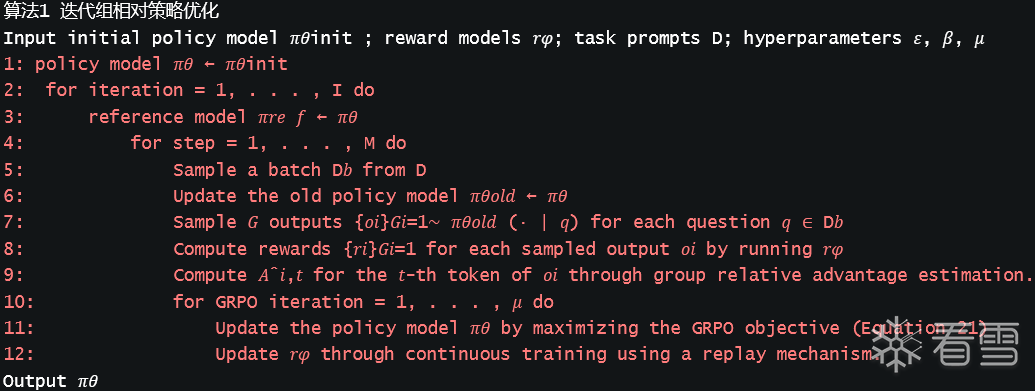
与在(2)中使用的 KL 惩罚项不同,我们用以下无偏估计量估计 KL 散度(Schulman, 2020):

该估计量保证为正。
结果监督 RL 与 GRPO
正式而言,对于每个问题 q,从旧策略模型 πθ_old 采样出一组输出 {o₁, o₂, ···, o_G}。然后,使用奖励模型对这些输出进行评分,得到对应的 G 个奖励 r = {r₁, r₂, ···, r_G}。随后,这些奖励会被归一化,
结果监督在每个输出 oᵢ 结束时提供归一化奖励,并将该归一化奖励作为所有 token 的优势 Âᵢ,ₜ,即:
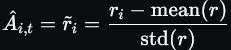
然后,通过最大化方程 (3) 中定义的目标来优化策略。
过程监督 RL 与 GRPO
结果监督仅在每个输出结束时提供奖励,这可能不足以有效监督复杂的数学任务。因此,我们参考 Wang et al. (2023b) 的方法,探索过程监督,它在每个推理步骤结束时提供奖励。
正式而言,给定问题 q 和 G 组采样输出 {o₁, o₂, ···, o_G},使用过程奖励模型对每个推理步骤进行评分,得到对应奖励:

其中,index(j) 表示第 j 步的结束 token 索引,Kᵢ 是第 i 个输出的总步骤数。然后,这些奖励同样被归一化:

随后,过程监督计算每个 token 的优势 Âᵢ,ₜ,其值为从当前 token t 到最终 token 的所有归一化奖励之和:

然后通过最大化方程 (3) 中定义的目标来优化策略。
迭代 RL 与 GRPO
随着强化学习训练的进行,旧的奖励模型可能无法有效监督当前的策略模型。因此,我们探索了 迭代 RL 与 GRPO。
如 算法 1 所示,在迭代 GRPO 过程中,我们基于策略模型的采样结果生成新的训练集,并使用重放机制(保留 10% 的历史数据)持续训练旧的奖励模型。然后,将参考模型设为当前策略模型,并用新的奖励模型持续训练策略模型。
训练与评估 DeepSeekMath-RL
我们基于 DeepSeekMath-Instruct 7B 进行强化学习训练。强化学习的训练数据来自 SFT 数据中的 GSM8K 和 MATH 相关的 Chain-of-Thought(CoT)格式问题,共约 144K 道题目。为了研究强化学习对缺乏训练数据的基准测试的影响,我们排除了其他 SFT 问题。奖励模型的训练集构建方式参考 Wang et al. (2023b)。
我们基于 DeepSeekMath-Base 7B 训练初始奖励模型,使用的学习率为 2e-5。对于 GRPO,我们将策略模型的学习率设为 1e-6,KL 系数设为 0.04。对于每个问题,我们采样 64 个输出,最大长度设为 1024,训练批次大小为 1024。策略模型在每个探索阶段后仅更新一次。
我们按照 DeepSeekMath-Instruct 7B 的评测方式评估 DeepSeekMath-RL 7B。其中,GSM8K 和 MATH(均采用 CoT 推理)被视为 域内任务,其他基准测试被视为 域外任务。
表 5 展示了采用 CoT 推理 和 工具辅助推理 的开源和闭源模型在中英文基准测试上的表现。结果发现:
- DeepSeekMath-RL 7B 在 GSM8K 和 MATH 上的准确率分别达到了 88.2% 和 51.7%,超越了 7B 至 70B 范围内的所有开源模型,并优于大多数闭源模型。
- DeepSeekMath-RL 7B 只在 GSM8K 和 MATH 的 CoT 格式指令微调数据上进行训练,其起点是 DeepSeekMath-Instruct 7B。尽管训练数据范围有限,但在所有评测指标上均优于 DeepSeekMath-Instruct 7B,展现了强化学习的有效性。
讨论
本节介绍我们在 预训练 和 强化学习实验 中的发现。
预训练中的经验总结
我们首先分享预训练的经验。除非另有说明,本节的训练设置均遵循 第 2.2.1 节 的设定。值得注意的是,DeepSeekMath 语料库 在本节中指的是 第二轮数据收集 生成的 89B-token 数据集。
代码训练有助于数学推理
一个流行但未经证实的假设认为:代码训练可以提升推理能力。我们尝试对此进行部分验证,尤其是在数学推理方面。
| 训练设置 | 训练tokens | w/o 使用数(tool use) | w/ 使用数(tool use) | |||||
| 普通 | 代码 | 数学 | GSM8K | MATH | CMATH | GSM8K+Python | MATH+Python | |
| 无阶段训练 | - | - | - | 2.9% | 3.0% | 12.3% | 2.7% | 2.3% |
| 二阶段训练 | ||||||||
| 阶段一:普通训练 | 400B | - | - | 2.9% | 3.2% | 14.8% | 3.3% | 2.3% |
| 阶段二:数学训练 | - | - | 150B | 19.1% | 14.4% | 37.2% | 14.3% | 6.7% |
| 阶段一:代码训练 | - | 400B | - | 5.9% | 3.6% | 19.9% | 12.4% | 10.0% |
| 阶段二:数学训练 | - | - | 150B | 21.9% | 15.3% | 39.7% | 17.4% | 9.4% |
| 单阶段训练 | ||||||||
| 数学训练 | - | - | 150B | 20.5% | 13.1% | 37.6% | 11.4% | 6.5% |
| 代码&数学混合训练 | - | 400B | 150B | 17.6% | 12.1% | 36.3% | 19.7% | 13.5% |
表6 研究代码在不同训练设置下如何影响数学推理。我们使用DeepSeek-LLM 1.3B进行实验,并通过少样本链式思维提示和少样本程序式思维提示,分别评估其在不使用工具和使用工具时的数学推理性能
实验结果表明,代码训练可以提高模型的数学推理能力,无论是否借助工具。
为了研究代码训练如何影响数学推理,我们进行了以下两阶段训练和单阶段训练的设置实验:
两阶段训练
- 代码训练 400B tokens → 数学训练 150B tokens:我们先使用 400B 代码 token 训练 DeepSeek-LLM 1.3B,然后在 150B 数学 token 上进行训练。
- 通用训练 400B tokens → 数学训练 150B tokens:作为对照实验,我们用 通用 token(从 DeepSeek-AI 构建的大规模语料库中采样) 代替代码 token,以研究代码 token 是否比通用 token 更适合数学推理。
单阶段训练
- 数学训练 150B tokens:直接训练 150B 数学 token。
- 混合训练 400B 代码 tokens + 150B 数学 tokens:由于数学训练会降低代码性能,我们试图通过混合训练来缓解灾难性遗忘问题,同时提升数学推理能力。
实验结果(见 表 6 和表 7):
代码训练能提升基于程序的数学推理能力(无论是两阶段训练还是单阶段训练)。
- 在 两阶段训练 中,代码训练本身已经显著提升了 GSM8K 和 MATH 在 Python 代码求解上的能力,后续的数学训练进一步提高了性能。
- 在 单阶段训练 中,混合代码和数学 token 有效缓解了灾难性遗忘问题,并增强了 代码能力(表 7) 以及 程序辅助数学推理能力(表 6)。
| 训练设置 | 训练tokens | MMLU | BBH | HumanEval(Pass@1) | MBPP(Pass@1) | ||
| 普通 | 代码 | 数学 | |||||
| 无阶段训练 | - | - | - | 24.5% | 28.1% | 12.2% | 13.0% |
| 二阶段训练 | |||||||
| 阶段一:普通训练 | 400B | - | - | 25.9% | 27.7% | 15.2% | 13.6% |
| 阶段二:数学训练 | - | - | 150B | 33.1% | 32.7% | 12.8% | 13.2% |
| 阶段一:代码训练 | - | 400B | - | 25.0% | 31.5% | 25.0% | 40.0% |
| 阶段二:数学训练 | - | - | 150B | 36.2% | 35.3% | 12.2% | 17.0% |
| 单阶段训练 | |||||||
| 数学训练 | - | - | 150B | 32.3% | 32.5% | 11.6% | 13.2% |
| 代码&数学混合训练 | - | 400B | 150B | 33.5% | 35.6% | 29.3% | 39.4% |
表7 研究代码和数学训练的不同设置如何影响模型在语言理解、推理和编码方面的性能。我们使用DeepSeek-LLM 1.3B进行实验。我们通过少样本链式思维提示在MMLU和BBH上评估模型。在HumanEval和MBPP上,分别进行零样本和少样本评估
| 模型 | 大小 | ArXiv语料库 | 英语测评 | 中文测评 | ||||||
| GSM8K | MATH | OCW | SAT | MMLUSTEM | CMATH | GaokaoMathCloze | GaokaoMathQA | |||
| DeepSeek-LLM | 1.3B | 无数学训练 | 2.9% | 3.0% | 2.9% | 15.6% | 19.5% | 12.3% | 0.8% | 17.9% |
| MathPile | 2.7% | 3.3% | 2.2% | 12.5% | 15.7% | 1.2% | 0.0% | 2.8% | ||
| ArXiv-RedPajama | 3.3% | 3.4% | 4.0% | 9.4% | 9.0% | 7.4% | 0.8% | 2.3% | ||
| DeekSeek-Coder-Base-V1.5 | 7B | 无数学训练 | 29.0% | 12.5% | 6.6% | 40.6% | 38.1% | 45.9% | 5.9% | 21.1% |
| MathPile | 23.6% | 11.5% | 7.0% | 46.9% | 35.8% | 37.9% | 4.2% | 25.6% | ||
| ArXiv-RedPajama | 28.1% | 11.1% | 7.7% | 50.0% | 35.2% | 42.6% | 7.6% | 24.8% |
表8 数学训练对不同arXiv数据集的影响。模型性能通过少样本链式思维提示进行评估
| ArXiv 语料库 | miniF2F-valid | miniF2F-test |
| 无数学训练 | 20.1% | 21.7% |
| MathPile | 16.8% | 16.4% |
| ArXiv-RedPajama | 14.8% | 11.9% |
表9 数学训练对不同arXiv语料库的影响,基础模型为DeepSeekCoder-Base-v1.5 7B。我们在Isabelle中评估从非正式到正式的证明
代码训练也能提升不借助工具的数学推理能力。
- 在 两阶段训练 中,代码训练的初始阶段已经带来了 适度提升,并加速了后续数学训练,使其达到最佳性能。
- 但在 单阶段训练 中,混合代码 token 和数学 token 会降低不借助工具的数学推理能力,可能原因是 DeepSeek-LLM 1.3B 规模较小,无法同时充分学习代码和数学数据。
ArXiv 论文似乎对提升数学推理能力无效
ArXiv 论文通常被作为数学预训练数据的一部分(Azerbayev et al., 2023; Lewkowycz et al., 2022a; Polu and Sutskever, 2020; Wang et al., 2023c)。然而,关于其对数学推理能力影响的详细分析尚未得到广泛研究。或许有些出人意料,根据我们的实验,ArXiv 论文似乎对提升数学推理能力无效。
我们在不同规模的模型上进行了实验,包括 DeepSeek-LLM 1.3B 和 DeepSeek-Coder-Base-v1.5 7B(Guo et al., 2024),并使用了不同处理流程的 ArXiv 语料进行训练:
- MathPile(Wang et al., 2023c):一个 89 亿(8.9B)token 的语料库,采用清理和过滤启发式规则构建,其中 85% 以上为科学领域的 ArXiv 论文;
- ArXiv-RedPajama(Computer, 2023):完整的 ArXiv LaTeX 文件,去除了导言、注释、宏和参考文献,总计 280 亿(28.0B)token。
在实验中,我们分别在 ArXiv 语料 上训练 DeepSeek-LLM 1.3B 1500 亿(150B)token,以及 DeepSeek-Coder-Base-v1.5 7B 400 亿(40B)token。结果表明,ArXiv 论文似乎并不能有效提升数学推理能力。当模型仅在 ArXiv 语料上训练时,它们在各种数学基准测试中未显示出显著提升,甚至在某些情况下表现下降。这些基准测试包括:
- 定量推理数据集(如 GSM8K 和 MATH,见表 8);
- 多项选择题测试(如 MMLU-STEM,见表 8);
- 形式化数学测试(如 miniF2F,见表 9)。
然而,这一结论仍存在一定 局限性,不能过于武断。我们尚未研究:
- ArXiv 语料对本研究未涵盖的特定数学任务(如定理的非正式化,即将正式的数学陈述或证明转换为非正式版本)的影响;
- 当 ArXiv 语料与其他类型的数据结合时,其潜在效果;
- ArXiv 论文的益处是否会在 更大规模的模型 上显现。
因此,仍需进一步探索,我们将在未来研究中继续深入分析。
强化学习的见解
迈向统一范式
在本节中,我们提出了 一个统一的范式 来分析不同的训练方法,如 SFT、RFT、DPO、PPO、GRPO,并进一步进行实验,探索该统一范式的关键因素。一般而言,训练方法关于参数 ???? 的梯度可以表示为:
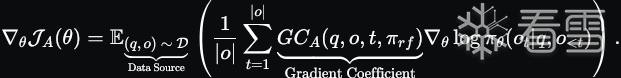
其中包含三个关键组成部分:
- 数据源 D:决定训练数据的来源;
- 奖励函数 ????????????:提供训练奖励信号的来源;
- 算法 A:处理训练数据和奖励信号,并计算 梯度系数 ????????,决定数据的惩罚或强化程度。
| 方案 | 数据源 | 奖励函数 | 梯度系数 |
| SFT | \[q, o \sim P_{sft}(Q, O)\] | - | 1 |
| RFT | \[q \sim P_{sft}(Q), \, o \sim \pi_{sft}(O \mid q)\] | Rule | Equation 10 |
| DPO | \(q \sim P_{sft}(Q), \, o^+, o^- \sim \pi_{sft}(O \mid q)\) | Rule | Equation 14 |
| Online RFT | \(q \sim P_{sft}(Q), \, o \sim \pi_{\theta}(O \mid q)\) | Rule | Equation 10 |
| PPO | \(q \sim P_{sft}(Q), \, o \sim \pi_{\theta}(O \mid q)\) | Model | Equation 18 |
| GRPO | \[q \sim P_{sft}(Q), \, \{o_i\}_{i=1}^{G} \sim \pi_{\theta}(O \mid q)\] | Model | Equation 21 |
表10 不同方法的数据来源和梯度系数。???????? ???? ????表示监督微调数据集的数据分布。???????????? ???? ???? 和 ????????分别表示在在线训练过程中监督微调模型和实时策略模型
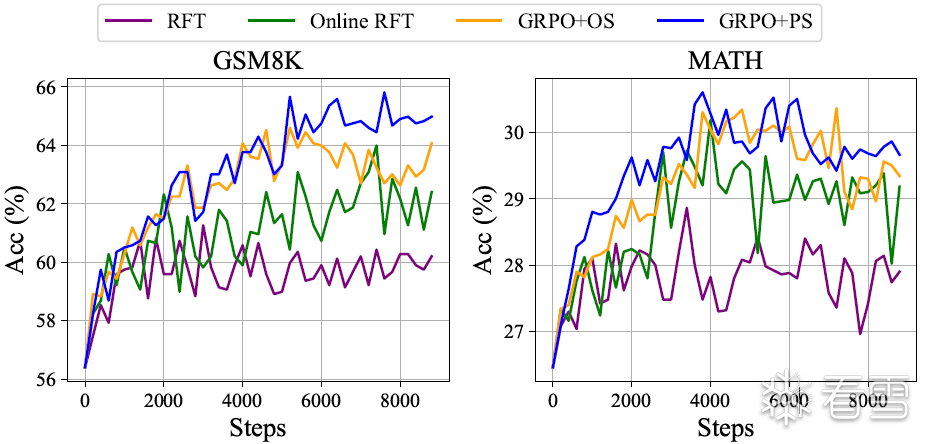
图5 DeepSeekMath-Instruct 1.3B模型在经过多种方法进一步训练后,在两个基准测试上的性能
基于这一范式,我们分析了几种典型的训练方法:
- 监督微调(SFT):SFT 在人工筛选的 SFT 数据上对预训练模型进行微调。
- 拒绝采样微调(RFT):RFT 在 SFT 基础上进一步微调,基于 SFT 生成的答案进行采样,并筛选正确答案进行训练。
- 直接偏好优化(DPO):DPO 在 SFT 模型的基础上,通过配对数据进行 DPO 损失优化。
- 在线拒绝采样微调(Online RFT):不同于 RFT,Online RFT 以 SFT 模型为起点,并通过 实时策略模型 生成的数据进行优化。
- PPO/GRPO:PPO/GRPO 以 SFT 模型为起点,并通过 实时策略模型 生成的数据进行强化训练。
我们在 表 10 中总结了这些方法的组成部分。详细的推导过程请参考 附录 A.1。
关于数据源的观察
我们将数据源分为 在线采样(online sampling) 和 离线采样(offline sampling) 两类:
- 在线采样 指训练数据来自 实时训练策略模型 的探索结果;
- 离线采样 指训练数据来自 初始 SFT 模型 生成的采样结果。
其中,RFT 和 DPO 采用 离线采样,而 Online RFT 和 GRPO 采用 在线采样。
如 图 5 所示,我们发现 Online RFT 在两个基准测试上显著优于 RFT。具体而言,Online RFT 在训练早期与 RFT 表现相当,但在后期取得 绝对优势,这表明 在线训练的优越性。
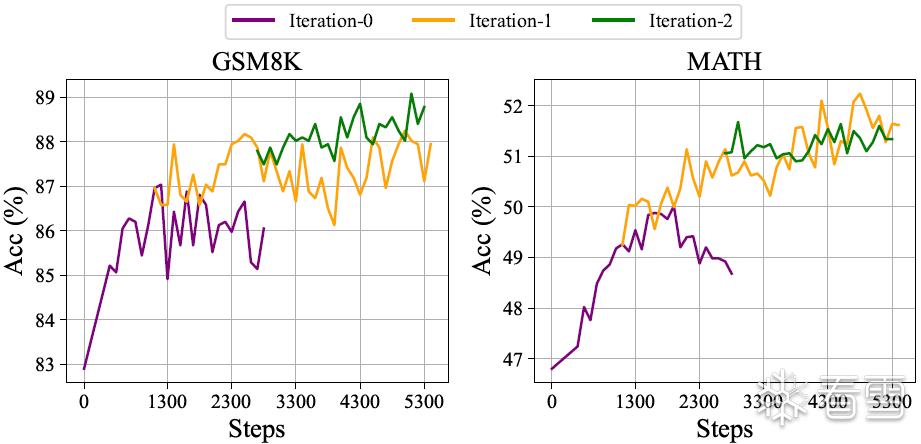
图6 使用DeepSeekMath-Instruct 7B进行迭代强化学习在两个基准测试上的性能
这可以直观理解:在训练初期,策略模型(actor)与 SFT 模型相似,采样数据的差异较小;但在训练后期,actor 采样的数据差异变大,而 实时数据采样 提供了更大的优势。
关于梯度系数的观察
算法处理奖励信号并生成梯度系数用于更新模型参数。在实验中,我们将奖励函数分为:
- “规则(Rule)”:基于答案正确性判断回答质量;
- “模型(Model)”:训练一个奖励模型来评分,每个回答的奖励值由奖励模型预测,而奖励模型的训练数据基于规则判断。
方程(10)和(21)揭示了 GRPO 与 Online RFT 之间的关键区别:
- GRPO 会根据奖励模型的分数 调整梯度系数,对不同程度的回答进行 差异化强化或惩罚;
- Online RFT 则没有这一特性,不会惩罚错误回答,所有正确回答的强化力度均相同。
如 图 5 所示,GRPO 显著优于 Online RFT,进一步验证了 调整梯度系数的有效性。此外,GRPO+PS 的表现优于 GRPO+OS,表明 使用细粒度、逐步感知的梯度系数更具优势。
此外,我们还探索了 迭代强化学习(iterative RL)。在实验中,我们进行了 两轮迭代,如 图 6 所示,迭代强化学习显著提升了模型性能,尤其是在第一轮迭代时效果最明显。
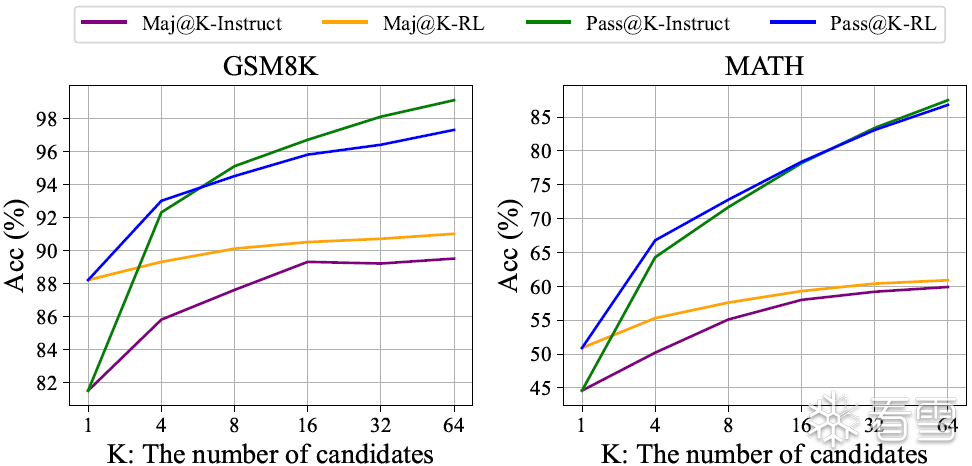
图7 SFT和RL DeepSeekMath 7B在GSM8K和MATH上的Maj@K和Pass@K(温度为0.7)。注意到RL提高了Maj@K,但没有提升Pass@K
为什么强化学习(RL)有效?
在本论文中,我们基于部分指令微调(instruction tuning)数据进行强化学习(RL),并在指令微调模型的基础上取得了显著的性能提升。为了进一步解释为什么强化学习有效,我们评估了 Instruct 模型和 RL 模型在两个基准测试上的 Pass@K 和 Maj@K 准确率。如图 7 所示,RL 提升了 Maj@K 的性能,但对 Pass@K 并无显著影响。这些发现表明,RL 通过使输出分布更加稳健来增强模型的整体性能,换句话说,这种改进似乎归因于提升了 TopK 中正确答案的概率,而非提升了模型的基本能力。同样,Wang 等人(2023a)在 SFT(监督微调)模型的推理任务中发现了错位问题,并表明可以通过一系列偏好对齐策略来提升 SFT 模型的推理能力(Song 等人,2023;Wang 等人,2023a;Yuan 等人,2023b)。
如何实现更有效的强化学习?
我们证明了强化学习在数学推理任务中表现良好,并提供了一个统一的范式来理解不同的代表性训练方法。在该范式下,所有方法都可以被概念化为直接或简化的强化学习技术。正如方程 5 所总结的,强化学习的关键组件包括 数据来源、算法和奖励函数。针对这三个方面,我们提出了一些未来的研究方向。
数据来源
数据来源是所有训练方法的原始材料。在强化学习的背景下,我们特指数据来源为 未标注的问题 以及从策略模型中采样的输出。在本论文中,我们仅使用指令微调阶段的问题,并采用 简单的 nucleus 采样 来生成输出。我们认为,这可能是导致我们的强化学习流程 仅提升了 Maj@K 性能 的一个潜在原因。未来,我们将探索在 分布外(out-of-distribution)问题 上应用我们的强化学习流程,并结合更先进的采样(解码)策略,例如基于 树搜索方法 的策略(Yao 等人,2023)。此外,高效推理技术(Kwon 等人,2023;Leviathan 等人,2023;Xia 等人,2023,2024)对于强化学习中的探索效率至关重要,这也是未来的一个重要研究方向。
算法
算法负责处理数据和奖励信号,并计算梯度系数以更新模型参数。根据方程 5,目前所有方法在一定程度上 完全信赖奖励函数的信号,以增加或减少特定 token 的条件概率。然而,奖励信号并非总是可靠的,尤其是在极其复杂的任务中。例如,即便是经过专业标注员精心标注的 PRM800K 数据集(Lightman 等人,2023),仍然存在大约 20% 的标注错误。因此,我们计划研究 对噪声奖励信号具有鲁棒性 的强化学习算法。我们认为,这种 弱到强(WEAK-TO-STRONG)对齐方法(Burns 等人,2023)将会对学习算法带来根本性的变革。
奖励函数
奖励函数是训练信号的来源。在强化学习中,奖励函数通常由神经奖励模型实现。我们认为奖励模型的研究可以从以下三个重要方向展开:
- 如何提升奖励模型的泛化能力。奖励模型必须能够 有效泛化,以处理分布外的问题和高级解码输出,否则强化学习可能仅仅稳定了 LLM 的输出分布,而未能提升其基本能力。
- 如何反映奖励模型的不确定性。不确定性可能成为 弱奖励模型 和 弱到强学习算法 之间的桥梁。
- 如何高效构建高质量的过程奖励模型,以提供 细粒度的训练信号,提升推理过程的优化效果(Lightman 等人,2023;Wang 等人,2023b)。
结论、局限性与未来工作
我们提出了 DeepSeekMath,其在竞赛级数学基准测试(MATH benchmark)上超越了所有开源模型,并接近闭源模型的性能。DeepSeekMath 以 DeepSeek-Coder-v1.5 7B 作为初始化模型,并经过 500B token 的持续训练,其中 120B 数学 token 来源于 Common Crawl。
我们进行了广泛的消融研究,结果表明 网页数据 具有极大的潜力,可用于构建高质量的数学数据,而 arXiv 数据的贡献并未达到预期。此外,我们提出了一种 Group Relative Policy Optimization(GRPO),这是一种 PPO(Proximal Policy Optimization) 的改进版本,该方法在减少内存消耗的同时,显著提升了数学推理能力。实验结果表明,即使 DeepSeekMath-Instruct 7B 在基准测试中已达到较高分数,GRPO 仍然能带来显著提升。
同时,我们提供了一个统一的范式来理解一系列训练方法,并总结了若干 提升强化学习有效性的潜在方向(见 5.2.3)。
尽管 DeepSeekMath 在定量推理基准测试上取得了令人印象深刻的成绩,但其在 几何和定理证明任务 上的能力仍然 弱于闭源模型。例如,在我们的测试过程中,该模型 无法处理三角形和椭圆相关问题,这可能表明 预训练和微调阶段的数据选择存在偏差。
此外,由于模型规模的限制,DeepSeekMath 的少样本(few-shot)能力不如 GPT-4。GPT-4 在 few-shot 输入下可以大幅提升性能,而 DeepSeekMath 在 zero-shot 和 few-shot 评估中的表现基本相同。
未来,我们将进一步优化 数据选择流程,以构建更高质量的预训练数据。同时,我们也将探索 5.2.3 节 中提出的方向,以进一步提升 LLM 的强化学习效果。